


Banks Act, 1990 (Act No. 94 of 1990)RegulationsRegulations relating to BanksChapter II : Financial, Risk-based and other related Returns and Instructions, Directives and Interpretations relating to the completion thereof23. Credit risk: monthly returnDirectives and interpretations for completion of monthly return concerning credit risk (Form BA 200)Subregulation (18) Calculation of counterparty credit exposure or EAD in terms of the standardised approachSubregulation (18)(a) Matters relating to the exposure amount or EAD |
| (a) | Matters relating to the exposure amount or EAD |
A bank that adopted the standardised approach for the measurement of the bank’s exposure to counterparty credit risk—
| (i) | shall calculate its relevant exposure to counterparty credit risk or the relevant EAD amount in respect of each relevant netting set through the application of the formula specified below: |
The exposure amount or EAD shall be equal to—
alpha* (RC + PFE)
where:
| alpha | is equal to 1.4 |
| RC | is the relevant replacement cost, calculated in accordance with the relevant requirements specified in subparagraph (ii) below |
| PFE | is the relevant potential future exposure amount, calculated in accordance with the relevant requirements specified in subparagraph (iii) below |
| (ii) | shall calculate the relevant replacement cost component of the formula specified in subparagraph (i) above in accordance with the requirements specified in this subparagraph (ii), provided that— |
| (A) | the bank shall calculate the replacement cost amount at the level of each relevant netting set, provided that— |
| (i) | when the bank owes the relevant counterparty money, the bank has no replacement cost, since the bank will be able to instantly replace its trades and sell collateral at current market prices without any loss or cost to the bank in the case that the counterparty defaults; |
| (ii) | the relevant replacement cost shall in no case be less than zero; |
| (iii) | when the bank enters into multiple margin agreements that apply to a single netting set, the bank shall divide the netting set into sub-netting sets that align with their respective margin agreement; |
| (iv) | when the bank holds excess collateral, even in the absence of a margin agreement, or the bank has out-of-the-money trades that can further protect the bank from an increase in its relevant counterparty exposure, the bank may reduce the relevant potential future exposure add-on amount with such over-collateralisation or negative mark-to market value, but the said over-collateralisation or negative mark-to-market value shall in no case affect the replacement cost envisaged in this subparagraph (ii); |
| (B) | the bank shall treat any bilateral transaction with a one-way margining agreement in favour of the bank’s counterparty, that is, when the bank is required to post, but does not collect, collateral, as an unmargined transaction; |
| (C) | the bank shall only apply any form of netting between amounts in the calculation of the relevant replacement cost component when all the conditions specified in paragraph (b) below are met; |
| (D) | for purposes of these Regulations, in the case of margined trades or transactions— |
| (i) | the relevant replacement cost shall be the largest exposure amount to the relevant counterparty without triggering a call for variation margin, taking into account the relevant mechanics of collateral exchange in the bank’s relevant margining agreement, including, for example, “Threshold”, “Minimum Transfer Amount” and “Independent Amount” arrangements, which may be factored into a call for variation margin; |
| (ii) | the independent collateral amount, denoted by ICA— |
| (aa) | means— |
| (i) | collateral other than variation margin posted by the relevant counterparty, which the bank may seize when the counterparty defaults, the amount of which does not change in response to the value of the transactions it secures; and/or |
| (ii) | the Independent Amount, denoted by IA, parameter, as often defined in standardised documentation; |
| (bb) | may change in response to factors such as the value of the collateral or a change in the number of transactions in the netting set; |
| (iii) | the net independent collateral amount, denoted by NICA— |
| (aa) | means— |
| (i) | the relevant aggregate amount of segregated or unsegregated collateral posted by the relevant counterparty, less the aggregate amount of unsegregated collateral posted by the bank; or |
| (ii) | the amount of collateral that the bank may use to offset its exposure when the relevant counterparty defaults; |
| (bb) | shall not include collateral that the bank has posted to a segregated, bankruptcy remote account, which presumably would be returned upon the bankruptcy of the counterparty; |
| (cc) | takes into account the differential of the IA required for the bank minus the IA required for the relevant counterparty; |
| (iv) | the relevant replacement cost may be stated mathematically as: |
RC = max{V minus C; TH plus MTA minus NICA; 0}
where:
| V | is the value of the relevant derivative transactions in the netting set |
| C | is the haircut value of the net collateral held, which shall be calculated in accordance with the NICA methodology specified hereinbefore, provided that for purposes of this calculation the value of non-cash collateral posted by the bank to its counterparty shall be increased by, and the value of the non-cash collateral received by the bank from its counterparty shall be decreased by, the relevant haircuts specified in these Regulations from time to time in respect of repo-style transactions |
| TH | is the positive threshold before the counterparty is required to send the bank collateral |
| MTA | is the minimum transfer amount applicable to the relevant counterparty |
TH + MTA – NICA:
is the largest exposure amount to the relevant counterparty without triggering a call for variation margin, and it contains levels of collateral that have to be maintained at all times.
For example, without initial margin or IA, the largest exposure that would not trigger a variation margin call is the threshold plus any minimum transfer amount.
In the formulation, NICA is subtracted from TH + MTA in order to fully reflect both the actual level of exposure that would not trigger a margin call and the effect of collateral held and/or posted by the bank.
The aforesaid calculation is subject to a floor amount of zero, recognising that the bank may hold NICA in excess of TH + MTA, which could otherwise result in a negative replacement cost;
| (v) | the purpose of— |
| (aa) | the calculation of the relevant replacement cost is to capture the probable loss that is likely to occur if the counterparty defaults, assuming that the closeout and replacement of transactions occur instantaneously; |
| (bb) | the calculation of the relevant potential future exposure add-on in terms of the requirements specified in subparagraph (iii) below is to capture the potential change in the value of the trades during the so-called margin period of risk, that is, the period between the last exchange of collateral before default and the replacement of the trades in the market; and |
| (cc) | the haircut applicable to non-cash collateral is to reflect the potential change in the value of the collateral during the relevant margin period of risk; |
| (E) | for purposes of these Regulations, in the case of unmargined transactions, that is, when no variation margin is exchanged, although collateral other than variation margin may be exchanged— |
| (i) | the relevant replacement cost shall be the greater of: |
| (aa) | the current market value of the relevant derivative contracts less the net haircut collateral held by the bank, if any; or |
| (bb) | zero, |
which may be stated mathematically as:
replacement cost (RC) = max{V – C; 0}
where:
| V | is the value of the relevant derivative transactions in the netting set |
| C | is the haircut value of the net collateral held, which shall be calculated in accordance with the NICA methodology specified in subparagraph (ii)(D)(iii) above, provided that for purposes of this calculation the value of non-cash collateral posted by the bank to its counterparty shall be increased by, and the value of the non-cash collateral received by the bank from its counterparty shall be decreased by, the relevant haircuts specified in these Regulations from time to time in respect of repo-style transactions |
| (ii) | the purpose of— |
| (aa) | the calculation of the relevant replacement cost is to capture the probable loss that is likely to occur if the counterparty defaults and all relevant transactions are closed out immediately; |
| (bb) | the calculation of the relevant potential future exposure add-on in terms of the requirements specified in subparagraph (iii) below is to capture the potential conservative increase in exposure over a one-year time horizon from the relevant reporting or calculation date; and |
| (cc) | the haircut applicable to non-cash collateral is to reflect the potential change in the value of the collateral during the said one year time period; |
| (F) | when a single margin agreement applies to several netting sets, and, as such, it is problematic to allocate any common collateral to individual netting sets, the bank shall calculate the relevant replacement cost as the sum of two components, as follows: |
| (i) | the unmargined current exposure of the bank to the relevant counterparty, aggregated across all the relevant netting sets within the margin agreement, reduced by the positive current net collateral, that is, collateral is subtracted only when the bank is a net holder of collateral, provided that the said net collateral amount available to the bank shall include both VM and NICA; |
| (ii) | the current net posted collateral, if any, reduced by the unmargined current exposure of the relevant counterparty to the bank, aggregated across all the relevant netting sets within the margin agreement, which component can be non-zero only when the bank is a net poster of collateral; |
| (iii) | RC for the entire margin agreement is therefore calculated as follows: |
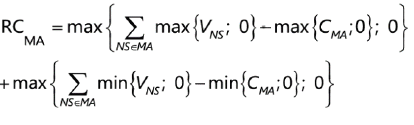
where:
the summation NSЄMA is across the netting sets covered by the relevant margin agreement
VNS is the current mark-to-market value of the netting set NS
CMA is the cash equivalent value of all the currently available collateral in terms of the relevant margin agreement
| (G) | when the bank obtained eligible collateral which is taken outside a netting set, but is available to the bank to offset losses due to counterparty default on one netting set only, the bank shall treat such collateral as an independent collateral amount associated with the netting set and used within the calculation of replacement cost in terms of the provisions of item (E) above when the netting set is unmargined and in terms of the provisions of item (D) above when the netting set is margined, provided that— |
| (i) | the bank shall treat any eligible collateral which is taken outside a netting set and that is available to the bank to offset losses due to counterparty default on more than one netting set as collateral taken under a margin agreement applicable to multiple netting sets, as envisaged in item (F) above; |
| (ii) | when eligible collateral is available to offset losses on non-derivatives exposures as well as exposures determined using the standardised approach set out in this subregulation (18), the bank shall only use that portion of the collateral assigned to the derivatives to reduce the bank’s relevant exposure to derivative instruments; |
| (H) | in all cases the relevant exposure amount or EAD for a margined netting set shall be capped at the relevant exposure amount or EAD of the same netting set calculated on an unmargined basis; |
| (iii) | shall calculate the relevant potential future exposure add-on component of the formula specified in subparagraph (i) above in accordance with the relevant requirements specified in this subparagraph (iii), provided that— |
| (A) | for purposes of these Regulations— |
| (i) | the relevant potential future exposure add-on shall consist of two distinct components, namely— |
| (aa) | an aggregate add-on component— |
| (i) | which consists of add-ons calculated for each relevant asset class within a given netting set, that is, the bank shall calculate the relevant add-on for each asset class through the application of the relevant specified asset class-specific formulae that represent a stylised Effective EPE calculation under the assumption that all trades in the asset class have zero current mark-to-market value, that is, all trades are assumed to be at-the-money; |
| (ii) | which add-on varies, based on the number of hedging sets that are available within an asset class, and which variations account for basis risk and differences in correlations within the relevant asset classes; and |
| (bb) | a multiplier that allows for the recognition of excess collateral or negative mark-to-market value for the relevant transactions; |
| (ii) | the relevant potential future exposure may be stated mathematically as: |
Potential future exposure (PFE) = multiplier * AddOnaggregate
where:
| multiplier | is a function of three inputs: V, C and AddOnaggregate, which multiplier shall be subject to a floor of 5 per cent of the relevant PFE add-on |
| AddOnaggregate | is the aggregate add-on component |
| (iii) | the bank shall duly separate all relevant trades within each relevant asset class into the relevant required hedging sets and aggregate all the relevant trade-level inputs at the hedging set level and finally at the asset class level, in accordance with the relevant formulae and requirement |
s specified in this subparagraph (iii);
| (iv) | in the case of interest rate derivative instruments— |
| (aa) | a hedging set shall consist of all relevant derivatives that reference interest rates of the same currency, such as, for example, ZAR, USD, EUR, JPY, etc., that is, there shall be a separate hedging set in respect of each relevant currency; |
| (bb) | hedging sets shall be further divided into maturity categories in respect of which long and short positions in the same hedging set may fully offset each other within maturity categories, but only partial offsetting shall be permitted across maturity categories; |
| (v) | in the case of foreign exchange derivative instruments, a hedging set shall consist of all relevant derivatives that reference the same foreign exchange currency pair, such as, for example, USD/ZAR, USD/Yen, Euro/Yen, or USD/Euro, that is, there shall be a separate hedging set in respect of each relevant currency pair, in respect of which full offsetting shall be permitted for long and short positions in the same currency pair, but no offsetting shall be permitted across currency pairs; |
| (vi) | in the case of credit derivative instruments and equity derivative instruments, a single hedging set shall apply for each relevant asset class, in respect of which full offsetting shall be permitted for derivatives that reference the same entity (name or index), but only partial offsetting shall be permitted between derivatives referencing different entities; |
| (vii) | in the case of commodity derivative instruments, four hedging sets shall apply, one for each different class of commodity, that is, one each for energy, metals, agricultural, and other commodities, and in respect of which— |
| (aa) | full offsetting shall be permitted between derivatives referencing the same commodity within the same hedging set; |
| (bb) | partial offsetting shall be permitted between derivatives referencing different commodities; and |
| (cc) | no offsetting shall be permitted between different hedging sets; |
| (viii) | in respect of each relevant asset class, basis transactions and volatility transactions shall form separate hedging sets within their respective asset classes, as set out below, in respect of which the relevant specified factors shall apply: |
All relevant—
| (aa) | derivatives that reference the basis between two risk factors and are denominated in a single currency, which shall for purposes of this subregulation (18) be referred to as basis transactions, shallbe treated within separate hedging sets within the relevant corresponding asset class, that is, all basis transactions of a netting set that belong to the same asset class and reference the same pair of risk factors shall form a single hedging set, provided that— |
| (i) | derivatives with two floating legs that are denominated in different currencies, such as, for example, cross-currency swaps, shall be treated as non-basis foreign exchange contracts; |
| (ii) | within each relevant hedging set, long and short positions shall be determined with respect to the relevant basis; |
| (iii) | the bank shall in the case of hedging sets that consist of basis transactions multiply the relevant specified factor denoted by SFi(a), applicable to a given asset class, by one-half; |
| (bb) | derivatives that reference the volatility of a risk factor, which shall for purposes of this subregulation (18) be referred to as volatility transactions, shall be treated within separate hedging sets within the relevant corresponding asset class, that is, all equity volatility transactions, for example, shall form a single hedging set, provided that the bank shall in the case of hedging sets that consist of volatility transactions multiply the relevant specified factor denoted by SFi(a), applicable to a given asset class, by a factor of five; |
| (ix) | the bank shall determine and allocate the primary risk factor or factors in respect of each relevant transaction to one or more of the following five asset classes: |
| (aa) | interest rate; |
| (bb) | foreign exchange; |
| (cc) | credit; |
| (dd) | equity; or |
| (ee) | commodity; |
| (x) | the bank shall allocate all its relevant derivative transactions to an appropriate asset class based on its primary risk driver or reference underlying instrument, such as, for example, an interest rate curve for an interest rate swap, a reference entity for a credit default swap, or a foreign exchange rate for a FX call option, provided that— |
| (aa) | in the case of more complex trades that may have more than one risk driver, such as, for example, multi-asset or hybrid derivatives, the bank shall take into account the relevant sensitivities and volatility of the underlying to determine the relevant primary risk driver; |
| (bb) | subject to such conditions as may be specified in writing by the Authority, the Authority may direct the bank to allocate complex trades to more than one asset class, which will result in the same position being included in multiple asset classes, in which case the bank shall determine the appropriate sign and delta adjustment of the relevant risk driver for each relevant asset class to which the position is allocated; |
| (xi) | the bank shall in all relevant cases calculate an adjusted notional amount based on the actual notional amount or price of the transaction, at the trade level, provided that— |
| (aa) | in the case of interest rate derivative instruments or credit derivative instruments, the said trade-level adjusted notional amount for trade i of asset class a, which is denoted by di(a) — |
| (i) | shall duly take into account both the size of a position and its maturity dependency, if any; |
| (ii) | shall incorporate any relevant specified measure of duration; |
| (iii) | shall be the product of the trade notional amount, converted to the relevant domestic currency, and the relevant specified duration, which is denoted by SDi, and calculated through the application of the formula specified below: |
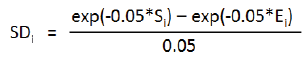
where:
| Si and Ei | are the respective start and end dates of the time period referenced by the interest rate or credit derivative, or, where such a derivative references the value of another interest rate or credit instrument, the time period determined on the basis of the relevant underlying instrument, subject to a floor of ten business days, provided that when the start date has already occurred, such as, for example, an ongoing interest rate swap, Si shall be equal to zero. |
For example, a European interest rate swaption with expiry of 1 year and the term of the underlying swap of 5 years has a start date (Si) of 1 year and an end date (Ei) of 6 years;
| (bb) | in the case of foreign exchange derivative instruments, the adjusted notional amount shall be the notional amount of the relevant foreign currency leg of the contract, converted to the relevant domestic currency, provided that when both legs of the foreign exchange derivative transaction are denominated in currencies other than the relevant domestic currency, the bank shall convert the notional amount of each leg to the relevant domestic currency and the leg with the larger domestic currency value shall be the adjusted notional amount; |
| (cc) | in the case of equity and commodity derivative instruments, the adjusted notional amount shall be equal to the product of the current price of one unit of the stock or commodity, such as, for example, a share of equity or barrel of oil, and the number of units referenced by the trade; |
| (dd) | when the trade notional amount is not stated clearly in the relevant contract, and fixed until maturity— |
| (i) | and the notional is a formula of market values, the bank shall apply the current market values to determine the relevant required trade notional amount; |
| (ii) | the bank shall in the case of interest rate and credit derivative contracts with variable notional amounts specified in the contract, such as amortising and accreting swaps, use the relevant time-weighted average notional over the remaining life of the derivative as the relevant required trade notional amount, |
Provided that the aforementioned requirements related to averaging do not apply to transactions in respect of which the notional varies due to price changes, such as, for example, foreign exchange, equity and commodity derivative contracts.
| (iii) | the bank shall in the case of leveraged swaps, convert the relevant value to the notional of an equivalent unleveraged swap. |
For example, when all rates in a swap are multiplied by a factor, the bank shall multiply the stated notional amount by that factor on the interest rates to determine the relevant required trade notional amount;
| (iv) | the bank shall in the case of a derivative contract with multiple exchanges of principal, multiply the notional amount with the number of exchanges of principal in the derivative contract to determine the relevant required trade notional amount; |
| (v) | the remaining maturity of a derivative contract that is structured such that on specified dates any outstanding exposure is settled and the terms are reset so that the fair value of the contract is zero, shall be the time until the next reset date; |
| (ee) | depending on whether the relevant transaction is a margined or an unmargined transaction, the bank shall apply to the relevant adjusted notional amount any relevant specified maturity factor, at the trade level, to duly reflect the time horizon appropriate for the relevant type of transaction; |
| (ff) | based upon the relevant long or short position and whether the trade is an option, CDO tranche or neither, the bank shall apply to the relevant trade-level adjusted notional amount any relevant specified delta adjustment as envisaged in sub-item (xii) below, in order to determine an effective notional amount: |
Provided that in the case of single-payment options the bank shall calculate the relevant required effective notional amount, that is, D = d * MF * δ, as follows:
| (i) | For European, Asian, American and Bermudan put and call options, the bank shall calculate the required delta by using the simplified Black-Scholes formula specified in sub-item (xii) below. In the case of Asian options, the underlying price must be set equal to the current value of the average used in the payoff. In the case of American and Bermudan options, the bank shall use the latest allowed exercise date as the exercise date Ti in the relevant specified formula; |
| (ii) | For Bermudan swaptions, the start date Si shall be equal to the earliest allowed exercise date, and the end date Ei shall be equal to the end date of the underlying swap; |
| (iii) | For digital options, the bank shall approximate the payoff of each bought or sold digital option with strike Ki via the “collar” combination of bought and sold European options of the same type, that is, call or put, with the strikes set equal to 0.95∙Ki and 1.05∙Ki. The size of the position in the collar components must be such that the digital payoff is reproduced exactly outside the region between the two strikes. The bank shall then separately compute the effective notional for the bought and sold European components of the collar, using the option formulae for the delta envisaged in sub-item (xii), and by using the exercise date Ti and the current value of the underlying Pi of the said digital option. The bank shall cap the absolute value of the digital-option effective notional by the ratio of the digital payoff to the relevant specified factor; |
| (iv) | When a trade’s payoff can be represented as a combination of European option payoffs, such as, for example, collar, butterfly/calendar spread, straddle, strangle, each relevant European option component shall be treated as a separate trade. |
For the purpose of calculating the relevant required effective notional amounts, multiple-payment options may be represented as a combination of single-payment options. In particular, interest rate caps/floors may be represented as the portfolio of individual caplets/floorlets, each of which is a European option on the floating interest rate over a specific coupon period. For each relevant caplet/floorlet, Si and Ti shall be the time periods starting from the current date to the start of the coupon period, while Ei shall be the time period starting from the current date to the end of the relevant coupon period;
| (gg) | in order to duly reflect volatility, the bank shall apply to each relevant effective notional amount such volatility factor as envisaged in sub-item (xiii) below; |
| (xii) | the bank shall apply to the aforesaid adjusted notional amount the relevant specified delta adjustment, at the trade level, to duly reflect the relevant direction of the transaction and its non-linearity, which delta adjustment is defined as follows: |
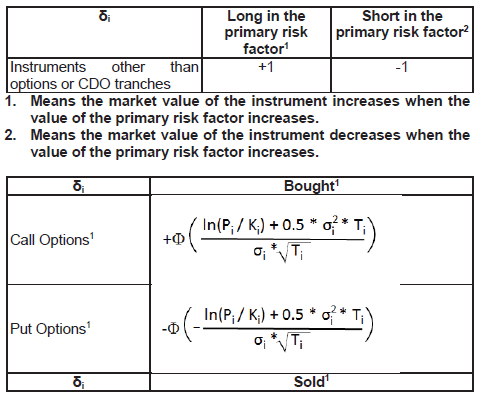

| (xiii) | in order to convert the relevant effective notional amount into an Effective EPE based on the measured volatility of the asset class, the bank shall apply to the aforesaid amount any relevant factor or factors specific to each asset class, which factor(s) is denoted by SFi(a) and has been calibrated to reflect the Effective EPE of a single at-the-money linear trade of unit notional and one-year maturity, in accordance with the relevant requirements specified in this subparagraph (iii); |
| (xiv) | in the case of— |
| (aa) | margined transactions— |
| (i) | the bank shall determine the minimum margin period of risk in accordance with the relevant requirements specified in table 1 below: |
Table 1
Minimum margin period of risk |
|
Non-centrally-cleared derivative transactions subject to daily margin agreements |
At least 10 business days |
Centrally cleared derivative transactions subject to daily margin agreements between clearing members and their clients |
5 business days |
Netting sets consisting of 5,000 transactions that are not with a central counterparty |
20 business days |
Netting sets with outstanding disputes as envisaged in subregulation (19)(e)(ii) |
Double the relevant specified margin period of risk |
| (ii) | the bank shall multiply the relevant adjusted notional amount at the trade level by: |
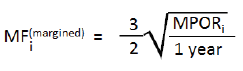
where:
| MPORi | is the margin period of risk appropriate for the relevant margin agreement containing the transaction i. |
| (bb) | unmargined transactions— |
| (i) | the minimum time risk horizon shall be the lesser of one year and the remaining maturity of the relevant derivative contract, subject to a floor of ten business days; |
| (ii) | the bank shall multiply the relevant adjusted notional amount at the trade level by: |
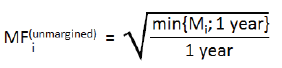
where:
| Mi | is the remaining maturity of transaction i, subject to a floor of ten business days |
| (xv) | in the case of credit derivative instruments, equity derivative instruments and commodity derivative instruments, the bank shall apply to the relevant PFE add-on calculation the relevant specified correlation parameters, denoted by ρi(a), to determine the appropriate degree of offset between individual trades in respect of the systemic and idiosyncratic components; |
| (xvi) | in order to determine the relevant date(s) to be applied— |
| (aa) | the maturity of a contract, denoted by Mi, shall in all cases be the latest date that the contract may still be active, provided that when a derivative contract has another derivative contract as its underlying, such as, for example, a swaption, that may be exercised into the relevant underlying contract, that is, the bank would assume a position in the underlying contract in the event of exercise, then the maturity of that contract shall be the final settlement date of the relevant underlying derivative contract; |
| (bb) | in the case of interest rate and credit derivative instruments, the start date and the end date of the relevant time period, respectively denoted by Si and Ei, shall be determined in accordance with the relevant dates specified in the contract, provided that when the derivative references the value of another interest rate or credit instrument, such as, for example, a swaption or bond option, the bank shall determine the relevant maturity category or time period based on the relevant underlying instrument; |
| (cc) | in the case of options, the latest contractual exercise date, denoted by Ti, shall be determined based on the relevant date specified in the contract, which period shall also be used to determine any relevant delta value; |
| (xvii) | the respective dates envisaged in subitem (xvi) above related to specified example types of transaction are set out in table 1 below: |
Table 1
Instrument |
Mi |
Si |
Ei |
Interest rate or credit default swap maturing in 10 years |
10 years |
0 |
10 years |
10-year interest rate swap, forward starting in 5 years |
15 years |
5 years |
15 years |
Forward rate agreement for time period starting in 6 months and ending in 12 months |
1 year |
0.5 year |
1 year |
Cash-settled European swaption referencing 5-year interest rate swap with exercise date in 6 months |
0.5 year |
0.5 year |
5.5 years |
Physically-settled European swaption referencing 5-year interest rate swap with exercise date in 6 months |
5.5 years |
0.5 year |
5.5 years |
10-year Bermudan swaption with annual exercise dates |
10 years |
1 year |
10 years |
Interest rate cap or floor specified for semiannual interest rate with maturity 5 years |
5 years |
0 |
5 years |
Option on a bond maturing in 5 years with the latest exercise date in 1 year |
1 year |
1 year |
5 years |
3-month Eurodollar futures that matures in 1 year |
1 year |
1 year |
1.25 years |
Futures on 20-year treasury bond that matures in 2 years |
2 years |
2 years |
22 years |
6-month option on 2-year futures on 20-year treasury bond |
2 years |
2 years |
22 years |
| (xviii) | the respective parameters to be applied in the required calculations of the respective add-on components envisaged in this subparagraph (iii) are set out in table 1 below: |
Table 1
Asset class |
Subclass |
Specified factor 1; 2 SFi(a) |
Correlation ρi(a) |
Option volatility |
Interest rate |
0.50% |
N/A |
50% |
|
Foreign exchange |
4.0% |
N/A |
15% |
|
Credit, single name |
AAA |
0.38% |
50% |
100% |
AA |
0.38% |
50% |
100% |
|
A |
0.42% |
50% |
100% |
|
BBB |
0.54% |
50% |
100% |
|
BB |
1.06% |
50% |
100% |
|
B |
1.6% |
50% |
100% |
|
CCC |
6.0% |
50% |
100% |
|
Credit, index |
IG3 |
0.38% |
80% |
80% |
SG4 |
1.06% |
80% |
80% |
|
Equity, single name |
32% |
50% |
120% |
|
Equity, index |
20% |
80% |
75% |
|
Commodity |
Electricity |
40% |
40% |
150% |
Oil/Gas |
18% |
40% |
70% |
|
Metals |
18% |
40% |
70% |
|
Agricultural |
18% |
40% |
70% |
|
Other |
18% |
40% |
70% |
| 1. | The bank shall in the case of a basis transaction hedging set multiply the relevant specified factor applicable to the relevant asset class by one-half. |
| 2. | The bank shall in the case of a volatility transaction hedging set multiply the relevant specified factor applicable to the relevant asset class by a factor of five. |
| 3. | Means investment grade. |
| 4. | Means speculative grade. |
| (B) | when the bank enters into multiple margin agreements that apply to a single netting set, the bank shall divide the netting set into sub-netting sets that align with their respective margin agreement; |
| (C) | when a single margin agreement applies to several netting sets, as envisaged in subparagraph (ii)(F) above, and collateral is exchanged based on the mark-to market values that are netted across all relevant transactions covered under the margin agreement, irrespective of the netting sets, and as such the collateral exchanged on a net basis may not be sufficient to cover the potential future exposure, the bank shall— |
| (i) | calculate the PFE add-on in accordance with the unmargined methodology; |
| (ii) | aggregate the netting set level PFEs through the application of the formula specified below: |
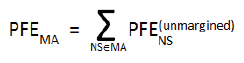
where:
![]()
is the PFE add-on for the netting set NS calculated in accordance with the relevant requirements related to unmargined transactions
| (D) | based on the aforesaid, in the case of interest rate derivative instruments— |
| (i) | the relevant add-on— |
| (aa) | shall be equal to the sum of the add-ons for each relevant hedging set transacted with a counterparty in a netting set; |
| (bb) | is intended to capture the risk of imperfect correlation between interest rate derivatives of different maturities; |
| (cc) | for a hedging set shall be calculated in two steps, as set out in subitems (iv) to (vii) below; |
| (ii) | based on the end-date of the relevant transactions, the bank shall allocate all relevant transactions into one of the following three maturity categories: |
| (aa) | less than one year; |
| (bb) | between one year and five years; and |
| (cc) | more than five years; |
| (iii) | the bank may— |
| (aa) | fully offset all relevant positions within a relevant specified maturity category; and |
| (bb) | partially offset relevant positions across the relevant specified maturity categories in accordance with the relevant requirements specified in this subparagraph (iii); |
| (iv) | the bank shall firstly calculate the effective notional amount for time bucket k of hedging set j, that is, currency j, through the application of the formula specified below: |
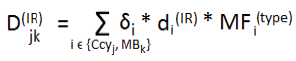
where:
![]()
is the effective notional amount refers to trades of currency j that belong to maturity bucket k
![]()
That is, the effective notional for each relevant time bucket and currency shall be equal to the sum of the trade-level adjusted notional amounts multiplied by—
| (aa) | the relevant delta adjustments; and |
| (bb) | the relevant maturity factor, |
specified hereinbefore;
| (v) | when the bank wishes— |
| (aa) | to offset relevant positions across maturity buckets, the bank shall, as part of the second step, aggregate across the relevant maturity buckets for each relevant hedging set through the application of the formulae specified below: |
![]()
where:
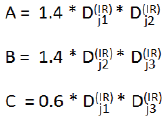
| (bb) | not to offset positions across maturity buckets, the bank shall, as part of the second step, calculate the relevant effective notional amount through the application of the formula specified below: |
![]()
| (vi) | the bank shall thereafter, as part of the second step, calculate the hedging set level add-on as the product of the effective notional and the relevant specified interest rate factor, through the application of the formula specified below: |
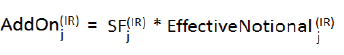
| (vii) | the bank shall then finally, as part of the second step, aggregate the said hedging set level add-ons by means of simple summation, through the application of the formula specified below: |
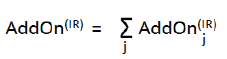
| (E) | based on the aforesaid, in the case of foreign exchange derivative instruments— |
| (i) | the add-on for a hedging set shall be the product of the absolute value of the relevant effective notional amount and the relevant specified factor, which is the same for all relevant FX hedging sets; |
| (ii) | the relevant effective notional amount of a hedging set shall be equal to the sum of all the relevant trade-level adjusted notional amounts multiplied by the relevant specified delta value; |
| (iii) | the adjusted notional amount is maturity independent and equal to the notional amount of the relevant foreign currency leg of the contract, converted to Rand; |
| (iv) | the add-on shall be calculated through the application of the formula specified below: |
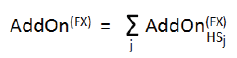
where:
the sum is taken over all the relevant hedging sets, denoted by HSj, included in the relevant netting set.
the add-on and the effective notional of the hedging set HSj are respectively calculated through the application of the formulae specified below:
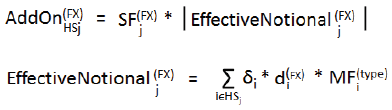
where:
| iЄHSj | means the relevant trades related to hedging set HSj |
that is, the effective notional for each relevant currency pair shall be equal to the sum of the relevant trade-level adjusted notional amounts multiplied by—
| (aa) | the relevant delta adjustment; and |
| (bb) | the relevant maturity factor, |
specified hereinbefore;
| (F) | based on the aforesaid, in the case of credit derivative instruments— |
| (i) | the bank shall firstly calculate an entity-level effective notional amount in respect of all relevant credit derivative instruments referencing either the same single entity or an index, in respect of which the bank may fully offset all relevant credit derivative instruments referencing that same single entity or index, through the application of the formula specified below: |
![]()
where:
| iЄEntityk | means the relevant trades related to entity k |
that is, the effective notional for each relevant entity shall be equal to the sum of the relevant trade-level adjusted notional amounts multiplied by—
| (aa) | the relevant delta adjustment; and |
| (bb) | the relevant maturity factor, |
specified hereinbefore;
| (ii) | the bank shall thereafter calculate the add-on for all the relevant positions referencing the aforesaid entity or index, through the application of the formula specified below: |
![]()
that is, the add-on for all the relevant positions referencing the aforesaid entity shall be the product of its effective notional amount and the relevant specified factor,
where:
| SFk(Credit) | is the relevant specified factor, which shall be determined as follows: |
| (aa) | in the case of any single name entity, based on the credit rating of the relevant reference entity; and |
| (bb) | in the case of any relevant index entity, based on whether that index is investment grade or speculative grade; |
| (iii) | with the exception of all relevant basis and volatility transactions, the bank shall then— |
| (aa) | group all the relevant entity-level add-ons within a single hedging set, in which full offsetting between two different entity-level add-ons shall not be permitted. |
Instead, a single-factor model is used that make provision for partial offsetting between the entity-level add-ons by dividing the risk of the credit derivatives asset class into a systemic component and an idiosyncratic component. The entity-level add-ons may fully offset each other in the systemic component, but no offsetting benefit is permitted in the idiosyncratic component.
The aforesaid two components are weighted by a correlation factor that determines the degree of offsetting/hedging benefit within the relevant credit derivatives asset class. The higher the correlation factor, the higher the importance of the systemic component, hence the higher the degree of offsetting benefits. Derivatives referencing credit indices shall be treated as though they were referencing single names, but a higher correlation factor applies;
| (bb) | calculate the relevant add-on through the application of the formula specified below: |
![]()
where:

| ρk(Credit) | is the relevant correlation factor specified for Entity k |
| (G) | based on the aforesaid, in the case of equity derivative instruments— |
| (i) | the bank shall firstly calculate an entity-level effective notional amount in respect of each relevant reference entity or index, in respect of which the bank may fully offset all relevant transactions related to the same reference entity or index, through the application of the formula specified below: |
![]()
where:
| iЄEntityk | means the relevant trades related to entity k |
that is, the effective notional for each relevant entity shall be equal to the sum of the relevant trade-level adjusted notional amounts multiplied by—
| (aa) | the relevant delta adjustment; and |
| (bb) | the relevant maturity factor, |
specified hereinbefore;
| (ii) | the bank shall thereafter calculate the add-on for all the relevant positions referencing the aforesaid entity or index, through the application of the formula specified below: |
![]()
that is, the add-on for all the relevant positions referencing the aforesaid entity or index shall be the product of its effective notional amount and the relevant specified factor,
where:
| SFk(Equity) | is the relevant specified factor |
| (iii) | the bank shall then— |
| (aa) | group all the relevant entity-level add-ons, in which full offsetting between two different entity-level add-ons shall not be permitted. |
Instead, a single-factor model is used to divide the risk into a systemic component and an idiosyncratic component in respect of each relevant reference entity or index. The entity-level add-ons may fully offset each other in the systemic component, but no offsetting benefit is permitted in the idiosyncratic component.
The aforesaid two components are weighted by a correlation factor which determines the degree of offsetting/hedging benefit. Derivatives referencing equity indices shall be treated as though they were referencing single entities, but a higher correlation factor applies for the systemic component;
| (bb) | calculate the relevant add-on through the application of the formula specified below: |
![]()
where:
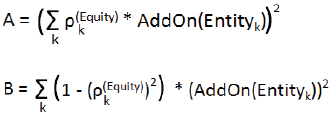
| ρk(Equity) | is the relevant correlation factor specified for Entity k |
| (H) | based on the aforesaid, in the case of commodity derivative instruments— |
| (i) | the bank— |
| (aa) | may in the calculation of the commodity type-level effective notional amount fully offset all relevant derivative transactions referencing the same type of commodity; |
| (bb) | shall calculate the effective notional amount of the commodity type k in hedging set j, through the application of the formula specified below: |
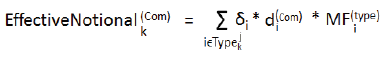
where:
| iϵTypejk | refers to the trades of commodity type k in hedging set j |
that is, the effective notional amount for each relevant commodity type shall be equal to the sum of the relevant trade-level adjusted notional amounts multiplied by—
| (i) | the relevant delta adjustment; and |
| (ii) | the relevant maturity factor, |
specified hereinbefore;
| (ii) | the bank shall then calculate the add-on for the relevant commodity type k in hedging set j, through the application of the formula specified below: |
![]()
| (iii) | within each relevant hedging set— |
| (aa) | a single factor model is used to divide the risk of the same type of commodities into a systemic component and an idiosyncratic component, in terms of which partial offsetting/hedging benefits is allowed within each relevant hedging set between the same type of commodities, but no offsetting/hedging benefits shall be applied between the respective hedging sets; |
| (bb) | the bank shall calculate the relevant add-on through the application of the formula specified below: |
![]()
where:

| ρj(Com) | is the relevant correlation factor in respect of hedging set j |
| (iv) | the bank shall then finally calculate the add-on for the relevant asset class by means of simple summation, through the application of the formula specified below: |
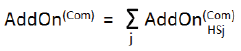
where the sum is taken over all the relevant hedging sets;
| (I) | when the relevant amount of collateral held— |
| (i) | is less than the net market value of the derivative contracts, that is, the position is under-collateralised, the current replacement cost is positive and the multiplier shall be equal to one, that is, the PFE component shall be equal to the full value of the aggregate add-on; |
| (ii) | is more than the net market value of the derivative contracts, that is, the position is over-collateralised, the current replacement cost is equal to zero, and the multiplier shall be less than one, that is, the PFE component shall be less than the full value of the aggregate add-on; |
| (J) | since out-of-the-money transactions do not represent a current exposure, and have less chance to go in-the-money, the aforesaid multiplier shall also be activated in the case of transactions with negative current value, that is, out-of-the-money transactions, which may be stated mathematically as: |

where:
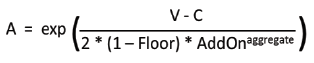
| exp(…) | equals to the exponential function |
| Floor | is 5 per cent |
| V | is the value of the derivative transactions in the relevant netting set |
| C | is the haircut value of the net collateral held |
| (K) | in all relevant cases, the relevant exposure amount or EAD in respect of a margined netting set shall be capped at the relevant exposure amount or EAD of the same netting set calculated on an unmargined basis; |
| (L) | the bank shall in no case apply any diversification benefits across asset classes, that is, the bank shall calculate the potential future exposure add-on amount for each relevant asset class within a given netting set by simply aggregating the relevant amounts, which may be stated mathematically as: |
![]()
| (b) | Matters related to bilateral netting |
A bank that adopted the standardised approach for the measurement of the bank’s exposure to counterparty credit risk may in the calculation of the relevant replacement cost component of a netting set, net transactions—
| (i) | subject to novation, in terms of which any obligation between the bank and its counterparty to deliver a given currency on a given value date is automatically amalgamated with all other obligations for the same currency and value date, legally substituting one single amount for the previous gross obligations; or |
| (ii) | subject to any legally valid form of bilateral netting not included in subparagraph (i) above, including any other form of novation: |
Provided that, in all relevant cases—
| (A) | the bank shall have in place a netting contract or agreement with the said counterparty that creates a single legal obligation, covering all included transactions, such that the bank would have either a claim to receive or an obligation to pay only the net sum of the positive and negative mark-to-market values of the said transactions in the event of counterparty failure to perform in accordance with the contractual agreement, irrespective whether or not the said failure relates to default, bankruptcy, liquidation or any other similar circumstances; |
| (B) | the bank shall have in place written and reasoned legal opinions confirming that in the event of a legal challenge the relevant courts and administrative authorities would find the bank’s exposure to be the said net amount in terms of— |
| (i) | the law of the jurisdiction in which the counterparty is incorporated or chartered, and when the foreign branch of a counterparty is involved, also in terms of the law of the jurisdiction in which the branch is located; |
| (ii) | the law that governs the individual transactions; and |
| (iii) | the law that governs any contract or agreement necessary to effect the said novation or netting; |
| (C) | when a national supervisor or regulator is not satisfied with the legal enforceability of the said agreement, neither counterparty shall apply netting in respect of the relevant transactions or contracts; |
| (D) | the bank shall have in place robust procedures in order to continuously monitor the legal characteristics of the said netting agreement for possible changes in relevant law that may affect the legal enforceability of the said agreement; |
| (E) | since the gross obligations are not in any way affected, no payment netting agreement, which is designed to reduce the operational costs of daily settlements, shall be taken into consideration in the calculation of the reporting bank’s exposure amount, EAD or required capital and reserve funds; |
| (F) | no contract containing walk-away clauses, that is, a provision that permits a non-defaulting counterparty to make only limited payments or no payment at all to the estate of a defaulter, even when the defaulter is a net creditor, shall be eligible for netting in terms of these Regulations. |
[Regulation 23(18)(a) substituted by section 3(l) of Notice No. 1427, GG44048, dated 31 December 2020 - effective 1 January 2021]